How to Use
This tool focuses on the application of probabilistic analysis in cause-effect chain modelling. A general probabilistic approach for ecological risk assessment, originating from ecotoxicology, is also available: Probabilistic effect analysis – The Species Sensitivity Distribution. Essential for the probabilistic modelling of cause-effect chains is state-of-the-art knowledge on these cause-effect chains, together with knowledge on probabilistic computation methods. This section provides more information on the following:
- General Approach
- Probabilistic modelling
- Probabilistic modelling and the precautionary principle
General Approach
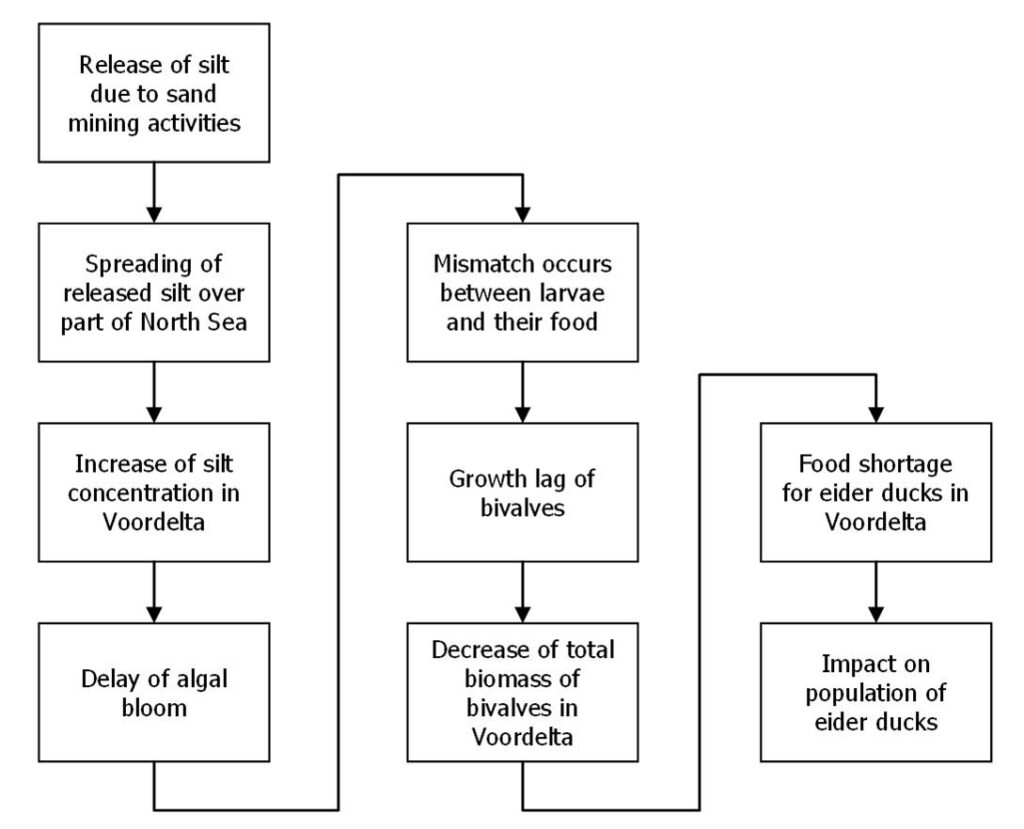
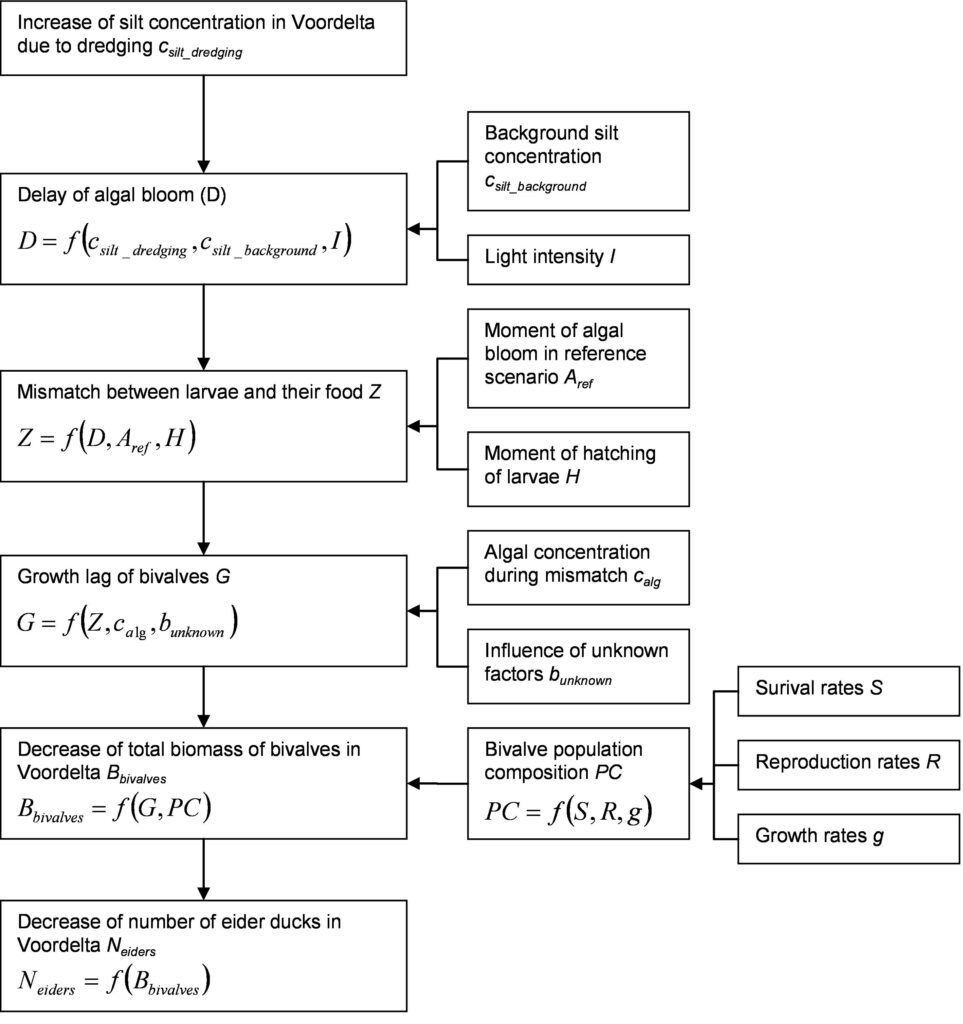
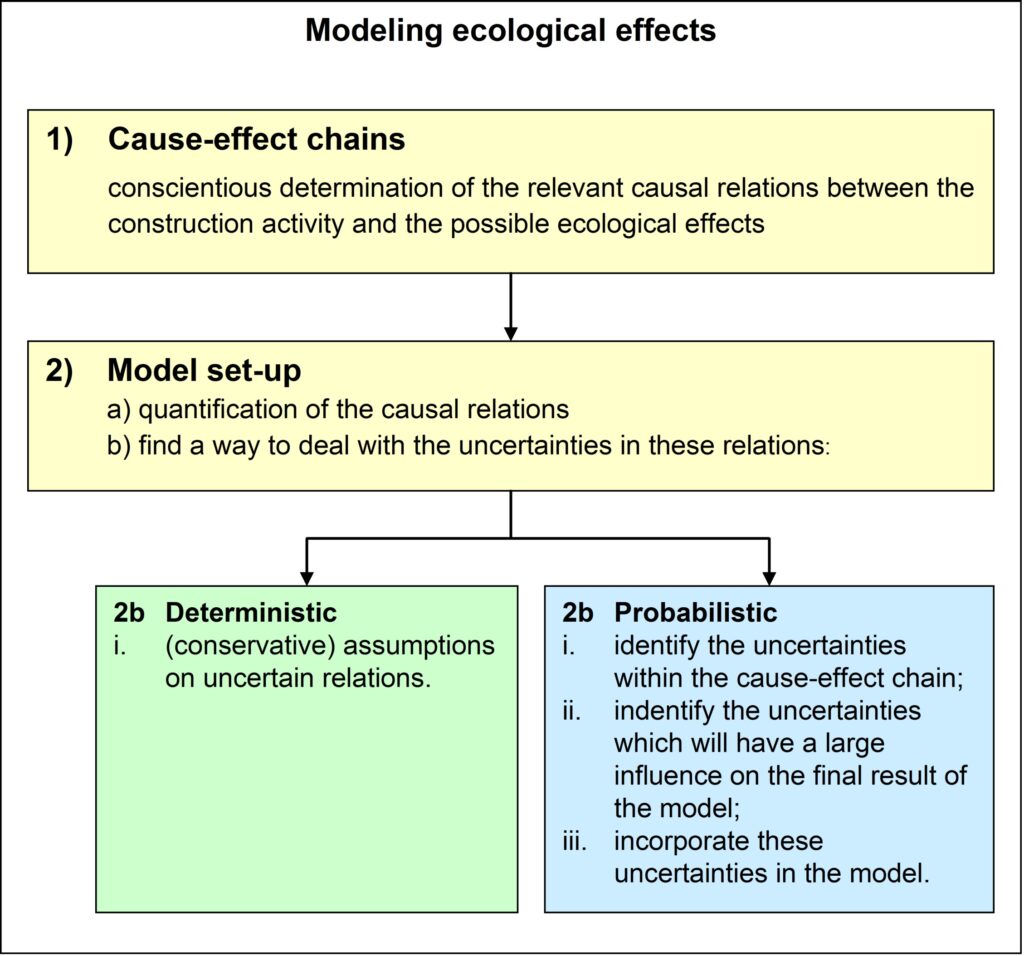
To be able to predict the ecological impact of a specific human intervention, the pathways by which this activity can interact with flora, fauna or ecosystems have to be known. For a deterministic as well as a probabilistic approach, the assessment of this interaction starts with insight into the cause-effect chains or networks. For a quantitative prediction of the effects of the above interaction, it is necessary to find out which quantitative relations exist between the actions and responses. For an example of a model set-up that can be used in a deterministic as well as a probabilistic approach, refer to the figure in the middle. The deterministic approach will yield a single value for each effect, the probabilistic approach an approximation of the probability distribution function.
Especially in the case of long impact-effect chains, the number of uncertainties will be very large, and they may grow throughout the process. Feedback loops may even lead to their unbounded amplification. A proper elaboration of the probabilistic analysis requires an overview of the uncertainties and their influence on the probability distribution function of the effect to be considered. Depending on its influence on the final result (compared to the effect of other uncertainties), it may be necessary to incorporate a specific uncertainty in the model. The relative influence of an uncertainty can sometimes be estimated analytically, otherwise model test-runs must give insight into the sensitivity of the result to a specific uncertainty variable.
To identify all relevant uncertainties, it is useful not only to look at the cause-effect chain ‘bottom-up’ but also ‘top-down’. In case of the example cause-effect chain (middle figure), this means that not only the question of ‘which factors may be affected by dredging’ (bottom-up) needs to be answered, but also ‘which factors influence the number of sea ducks’ (top-down). This may reveal more relevant factors than the bottom-up approach only, factors that have to be taken into account in the probabilistic analysis. The number of sea ducks, for instance, may not only depend on the possibly affected bivalve population, but also on a second food source. In case of an abundance of another food source, the potential decrease of the bivalve population does not necessarily result into a decline of the number of sea ducks.
Probabilistic modelling
Within cause-effect chains, several types of relations and uncertainties can be distinguished. Each type of uncertainty will require a specific method of incorporation in the probabilistic model. Although different data will be necessary for each hydraulic engineering project and each impact-effect chain, the same types of uncertainties will be encountered. Therefore, the method is formulated in such a way that it can be applied to different projects and different impact-effect chains.
For the overall modelling of ecological effects, in most cases, a Monte Carlo simulation and Social Cost Benefit Analysis is likely to be the most suitable probabilistic computation method. The Monte Carlo method relies on a repeated random sampling of input variables from probability density functions. The ecological impact is computed for a large number of input variable sets, using the (deterministic) quantitative relations of the cause-effect chain. Subsequently, all results can be analysed statistically, to yield probability density functions of the impact variables. For the random sampling, probability density functions have to be defined for each relevant stochastic input variable. How this can be done for different types of uncertainties is illustrated in the following examples:
1. Uncertainties on quantitative relations;
2. Uncertainties caused by natural variations;
3. Uncertainties caused by a lack of knowledge;
4. Uncertainties if impacts occur only under specific conditions.
Probabilistic modelling and the precautionary principle
The result of probabilistic modelling is a probability distribution function, in this case of an ecological effect. The inputs and the model used should be as realistic as possible. In view of the precautionary principle, however, the resulting probability distribution function should not give a too optimistic picture of reality. So, the probabilistic analysis should aim for ‘as realistic as possible, and certainly not too optimistic’. In the following, examples are elaborated on how one can deal with the precautionary principle in a probabilistic approach.
Precautionary principle: ‘if a reasonable suspicion exists that activities can have negative consequences for the environment, measures should be taken in order to prevent these consequences or, if the prevention of these consequences is not possible, to offer protection against these consequences’. This also means that a conservative assumption will be necessary for the quantitative effect analysis if no scientific evidence indicates that the real situation might be worse.
Example 1: Estimating probability density functions
In case of a probabilistic analysis, probability density functions (pdf’s) have to be estimated for several stochastic variables. If sufficient good quality data are available, an ‘indisputable pdf’ can be derived. However, if the quality or amount of data is insufficient for a clear interpretation, or the pdf has to be based on limited expert judgement, a conservative assumption on the pdf’s will be necessary in accordance with the precautionary principle. Please note that good insight in the interactions between input variables and their effect on the modelling results is necessary to be able to form a conservative assumption.
Example 2: Lack of knowledge
By using probabilistic modelling techniques, conservative assumptions can be prevented that have to be made when using a deterministic approach. An exception to this rule are uncertainties due to a lack of knowledge. In that case, the same assumptions as in the deterministic approach may have to be used. Also see above ‘Uncertainties caused by a lack of knowledge‘ and Visualising and managing uncertainties. In case of a complete lack of knowledge, even a worst-case assumption can be difficult or impossible.
